|
____________________________________________________________________________________________________
BENEFITS OF GAPPING THE CORE

If you require a stable inductor, a gap can reduce the flux density considerably. For instance, if the
initial permeability is 2000 and the core length is 100 mm (with a 1 mm gap),
the resulting effective permeability is reduced to a value of 95.24: -
\(\mu_e = \dfrac{\mu_i}{1+\dfrac{G\cdot\mu_i}{\ell_e}} \)
G is the gap,
\(\ell_e\) is the effective length of the magnetic core,
\(\mu_i\) and \(\mu_e\) are initial and effective permeabilities.
It becomes apparent that for materials with a decent value of initial
permeability and a reasonable gap, the effective permeability is
approximately \(\ell_e \div G\). With a 1mm gap, the
effective permeability is 100 (not far off from 95.24).
However, it's best to check the data sheet. For a
Ferroxcube planar E38/8/25 core-set,
you'll see this table below for various different materials including 3F3. Note that the core length (\(\ell_e\)) is 43.7 mm: -
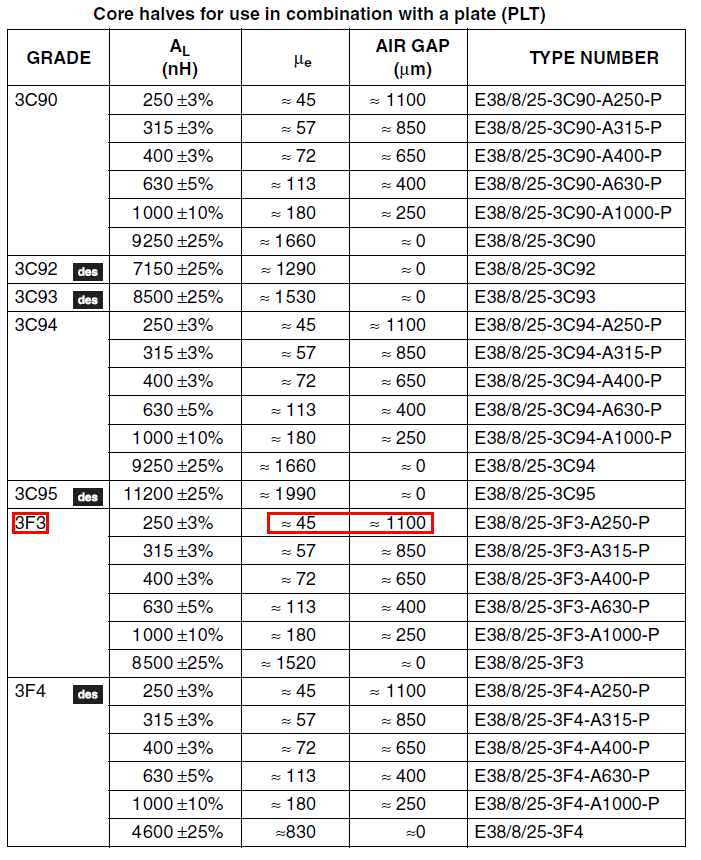
For 3F3 material with a 1.1 mm gap, \(\mu_e\) has fallen to 45 from 1520.
Note that for all the ferrite materials quoted above, the gapped \(\mu_e\) is the same - this is because gapping
makes "air" the dominant factor.
If we now calculate the H-field that produces 200 mT, what was previously 23 At/m is now proportionately higher by
1520 \(\div\) 45 at 777 At/m.
How does this benefit the design of an inductor?
-
If the inductor was designed to be 1000 µH (without a gap) we could wind it with 11 turns and get 1029 µH (near enough).
-
This is because the \(A_L\) value is 8500 nH for 1 turn and L rises with turns squared hence 11² x 8.5 µH = 1029 µH
-
Alternatively we could use the gapped \(A_L\) value of 250 nH. We would now need 64 turns to get an inductance of 1024 µH
For the same 200 mT flux density, comparing 23 At/m (11 turns) and 777 At/m (64 turns) means the gapped inductor realizes a peak
current that is about 5.8 times higher than the un-gapped inductor. However, more turns means more copper loss so there is give and take.
|